Egg Drop
I have had the idea to drop an egg from my window and not let it break using a parachute, but with a maths twist. I will think about how the parachute works, take measurements, and use maths to estimate what surface area my my parachute would need to reduce the impact force enough to give the egg a safe landing. Here are my notes:
Aim: To successfully land an egg onto concrete without breaking when dropping it out of my bedroom window using a parachute.
Background Info:
I was thinking about three forces in this experiment:
1. Gravity. The force that pulls objects towards the Earth.
2. Drag/air resistance. This is the force acting against gravity.
3. Impact. This the force of collision.
I know that force = mass * acceleration (F = ma)
The eggs had an average mass of 0.06kg
Acceleration is the rate at which the speed changes because of gravity (9.81m/s^2)
I am looking to increase drag to reduce acceleration and therefore reduce impact force.
Hypothesis:
If the drag produced by the egg + the parachute reduces the velocity enough; the force of impact will be lower then the force needed to break the egg. The force of drag acts against the force of gravity. The force of drag depends of the surface area of the parachute. The picture below shows the two forces acting in opposite directions.
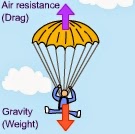
Image taken from: IGCSE Physics : c) Forces, movement, shape and momentum (igcsephysicsrevision15.blogspot.com)
Method:
I looked online for formulas to help me work out the surface area of parachute needed for a successful egg drop but this turned out to be really complicated, so I decided that trial and error might be best.
I already knew that F = ma (see above) and speed = distance/time
I also found out that:
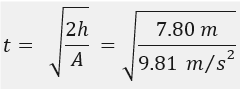
t = time (s), h = height of window, A = acceleration due to gravity
I used this to calculate how long I expected an egg to take to fall from my bedroom window: the results in real life were pretty close to this which was good taking into account human error in timing (see results).
Accel. Due to gravity: 9.81 m/s^2
Distance from window to floor: 3.90m
Predicted calculated time for regular egg to reach floor: 0.89s
Velocity of regular egg: 8.75 m/s (at impact)
Initial velocity: 0 m/s
I wanted to be able to calculate how much upwards force the parachute was providing and came across this formula (see below, and *). I was able to use the results from my experiment to calculate the drag. This is the upwards force that the parachute makes.
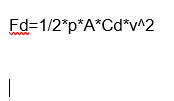
Where:
Fd = Air resistance or drag force in newtons (N)
p = Density of air, kg/m^3 = 1.29
A = cross sectional area of falling object, m^2 (area of parachute)
Cd = drag coefficient of parachute = 1.75
(standardized parachute drag coefficient)**
v = velocity of falling object, m/s (experimental data)
Using the data I know already I can say
Fd= (0.5)*1.29*0.73m^2*1.75* v^2
I made my parachute out of bin bags and strings and a freezer bag to hold the egg. I tested dropping the eggs in and out of freezer bags and it didn't seem to make any difference to how smashed they got or how fast they fell. To drop the egg and start the timer at the same time, we counted down from three steadily.
Results table:
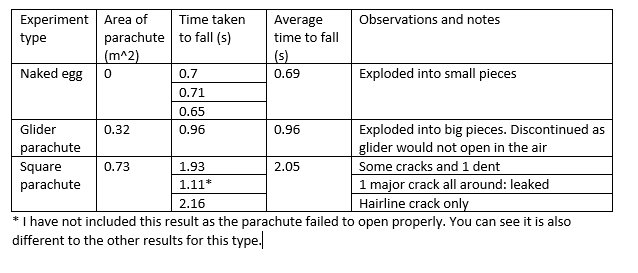
See below for some pictures of the experiment:
The first parachute design did not open, so I switched to a square one. This opened well on 2 out of 3 tries.
As described above, I used this formula to calculate the expected time taken for the naked egg drop
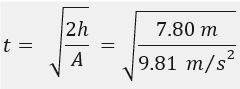
Predicted time for egg drop t = 0.89s
My experimental data is on average t = 0.69s
I think this is similar enough to believe my results are ok.
The average speed of the naked egg = 3.9m divided by 0.69s = 5.65m/s
The average speed of the parachute egg = 3.9m divided by 2.05s = 1.90 m/s
The downwards force of the falling egg is
Force(N) = mass*gravity
Force(N) = 0.6*9.81 = 5.89N
I have used formula no. 2 to calculate the upwards force of my parachute
Fd= (0.5)*1.29*0.73m2*1.75* 1.9^2
Fd = 2.97N
If I subtract one from the other I can say that the left-over force on my egg was 2.92N. This still made enough impact force to make a crack but not enough to smash the eggs when they had their parachutes on.
Conclusions:
In conclusion I have managed to reduce the force on the egg to 2.97N which is still not quite enough for the egg to remain perfectly intact at landing. If I were to do something differently it would be to increase the surface area of the parachute even more to increase drag which lowers the impact force more. Also to reduce human error for timing we could film the egg drop and then slow down the footage by a substantial amount to get a good measurement and then times the overall time by how much we slowed it down.
Above are some photos taken along the way. Some of my first attempts failed miserably but you quite literally have to break a few eggs to make scrambled eggs, or something like that. Or use a lime. As you can see, in the first trials I did use a lime as this was similar to an egg and less messy.